
INTEGRAL PROJECTIONS
An integral projection is a one-dimensional pattern, or signal, obtained through the sum of a given set of pixels along a given direction. Horizontal and vertical integral projections are most commonly used, although they can be applied on any direction.
Let i(x,y)
be an image (greyscale or color) and R(i) a
region in it (i.e., a set of pixels in i(x,y)),
the Vertical Integral Projection of R(i),
denoted by PVR(i), is a
discrete function:
PVR(i) : {ymin,
..., ymax} ® R
Defined by:
PVR(i) (y) = Mean(i(x,y));
" (x,y) Î R(i)
The Horizontal
Integral Projection of R(i), denoted by
PHR(i), is defined in a
similar way:
PHR(i) : {xmin,
..., xmax} ® R
PHR(i) (x)
= Mean(i(x,y)), " (x,y) Î R(i)
The Integral
Projection Along an Arbitrary Angle a,
denoted by PaR(i), is
defined as the vertical integral projection of R(i),
after applying to the image a rotation of a.
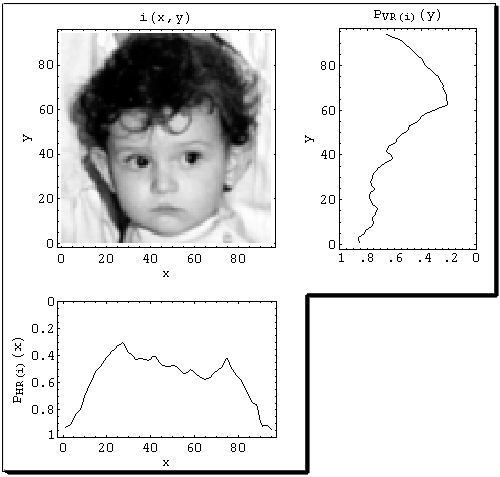
Sample image, with vertical
(right) and horizontal (down) integral projections.

Projection Models
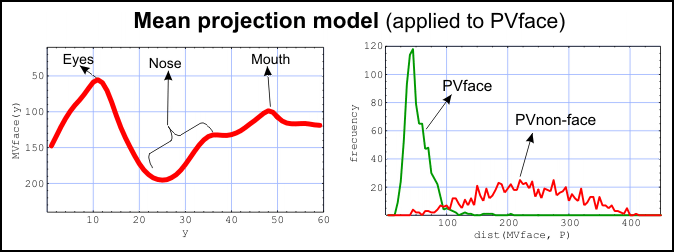
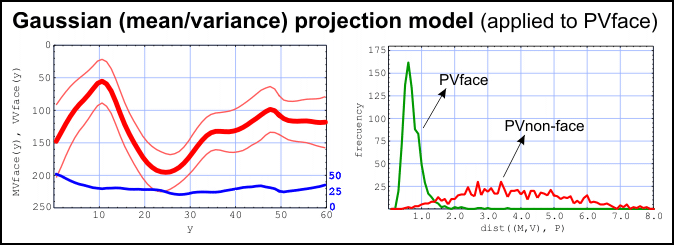
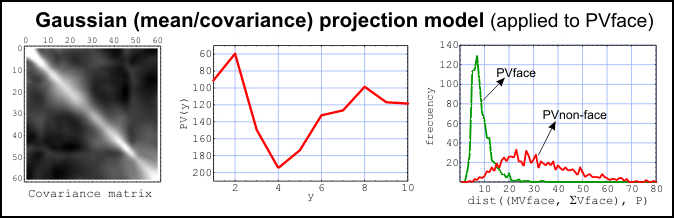
Rapid Alignment of Integral Projections

Facultad de Informática. Despacho 2.34
Campus de Espinardo. Universidad de Murcia
30100 Espinardo, Murcia (SPAIN)
Teléfono: +34 968
39 85 30
Fax: +34 968 36 41
51
E-mail: ginesgm@um.es