|
|
|
|
|
La seguridad en informática |
1.- Introducción Quizá antes sea importante mencionar algunos datos relacionados con la seguridad antes de comenzar con el desarrollo del tema. En el informe "Computer Crime Survey" del FBI, proporcionado por Secure Site E-News del 22 de mayo de 1999, de la compañía VeriSign, se dieron los siguientes datos: Se estudiaron 521 compañías de varias ramas de la industria y de diferentes tamaños. Estas están actualmente trabajando para que su sistema informático sea seguro. A la pregunta ¿qué tipo de tecnología de seguridad usa? Se contestó: A la pregunta ¿Cuál es el origen de un ataque? ¿Su organización provee servicio de comercio electrónico? Sí, el 29%.¿Su página ha tenido un acceso no autorizado en los últimos 12 meses? En un informe dado a conocer en unos cursos de criptografía industrial en Bélgica en junio de 1997, se mide la frecuencia de incidentes de seguridad de la información relacionada con sus causas. Frecuencia - RazónOtro aspecto importante a considerar es el crecimiento enorme que ha tenido internet, algunos datos importantes son los proporcionados por Paul Van Oorschot de Entrust Technologies en una conferencia del ciclo "The Mathematics of Public Key Cryptography" en junio de 1999: Se duplica él trafico de internet cada 100 días. En enero de 1999 hubo 150 millones de personas en línea, 75 de ellas en EEUU. El comercio mediante internet se duplica cada año. Podría llegar a un trillón de dólares lo comercializado en internet en el año 2002. La radio tardó 40 años y la televisión 10 años, para alcanzar 50 millones de usuarios a la red le ha bastado menos de cinco. Estos datos sólo son algunos de los que frecuentemente son dados a conocer por algún medio, y aunque algunos obedecen a intereses comerciales, lo que sí es verdadero es el enorme cambio que han tenido gran cantidad de actividades a raíz del uso de internet que incluso se ha considerado como el invento más importante de fin del siglo XX y de ahí lo primordial de todo lo relacionado con su seguridad. Siempre podremos encontrar razones para reafirmar la trascendencia que tiene la seguridad en los sistemas computerizados, seguidamente se da una introducción de cómo podemos atacar este problema. El diseñar una estrategia de seguridad depende en general mucho de la actividad que se esté desarrollando, sin embargo se pueden considerar los siguientes tres pasos generales: el primero crear una política global de seguridad, el segundo realizar un análisis de riesgos y el tercero aplicar las medidas correspondientes. Política global de seguridad: aquí se debe de establecer el estatus de la información para la empresa o la organización, debe de contener un objetivo general, la importancia de la tecnología de la información para la empresa, el período de tiempo de validez de la política, los recursos con que se cuenta, objetivos específicos de la empresa. Debe de establecerse la calidad de la información que se maneja según su objetivo, esto quiere decir que se establezca cuando o para quien la información debe ser confidencial, cuando debe verificarse su integridad y cuando debe de verificarse su autenticidad tanto de la información como de los usuarios. Análisis de riesgos: consiste en enumerar todo tipo de riesgos a los cuales esta expuesta la información y cuales son las consecuencias, los posibles atacantes entre persona, empresas y dependencias de inteligencia, las posibles amenazas etc., enumerar todo tipo de posible perdida, desde perdidas directas como dinero, clientes, tiempo etc., así como indirectas, créditos no obtenidos, perdida de imagen, implicación en un litigio, perdida de imagen, perdida de confianza etcétera. El riesgo se puede calcular por la formula riesgo = probabilidad ´ perdida, por ejemplo el riesgo de perder un contrato por robo de información confidencial es igual a la probabilidad de que ocurra el robo multiplicado por la perdida total en euros de no hacer el contrato. El riesgo de fraude en transacciones financieras es igual a la probabilidad de que ocurra el fraude por la perdida en euros de que llegara ocurrir ese fraude. Si la probabilidad es muy pequeña el riesgo es menor, pero si la probabilidad es casi uno, el riesgo puede ser casi igual a la perdida total. Si por otro lado la perdida es menor aunque la probabilidad de que ocurra el evento sea muy grande tenemos un riesgo menor. Por ejemplo la perdida de una transacción de 300 euros con una probabilidad muy grande de que ocurra al usar criptografía débil, el riesgo llega a ser menor por lo que depende de la política de seguridad para que este riesgo se asuma. Medidas de seguridad: esta parte la podemos plantear como la terminación de la toda la estructura de seguridad de la información. Una vez planteada una política de seguridad, o sea decir cuanto vale la información (en un análisis de riesgo), decir que tanto pierdo si le ocurre algo a mi información o que tanto se gana si está protegida, debemos de establecer las medidas para que cumpliendo con la política de seguridad las perdidas sean las menores posibles y que esto se transforme en ganancias, ya sean materiales o de imagen.
Las medidas que se pueden establecer se dividen según la tabla previa PF: vigilantes a la entrada del edificio, control en el acceso, protección al hardware, respaldo de datos, …En resumen debemos de mencionar que no existe un sistema computarizado que garantice al 100% la seguridad de la información, debido a la gran variededad de formas con que se puede romper la seguridad de un sistema. Sin embargo una buena planificación de la estrategia para dar seguridad a la información puede resultar desde la salvación de una empresa hasta la obtención de grandes ganancias directas en euros, o como ganancias indirectas mejorando la imagen y la seguridad de la empresa. Uno de los objetivos principales de estableces una política de seguridad es de reducir al mínimo los riegos posibles, implementando adecuadamente las diferentes medidas de seguridad. Enseguida repasamos algunas de las técnicas de seguridad que pertenecen a la criptografía, tratando de exponerlas de una forma simple de comprender. La palabra criptografía proviene del griego kryptos, que significa esconder y gráphein, escribir, es decir, escritura escondida. La criptografía ha sido usada a través de los años para mandar mensajes confidenciales cuyo propósito es que sólo las personas autorizadas puedan entender el mensaje. 2.- Introducción histórica Hace miles de años, el hombre comenzó a comunicarse con sus semejantes mediante un sistema estructurado de signos llamado lenguaje. La escritura, entendida como representación gráfica de algún lenguaje, surgió para poder conservar y transmitir los mensajes, permitiendo comunicar ideas sin necesidad de una interacción directa entre el emisor y el receptor. En muchos casos emisor y receptor son el mismo individuo, pues la escritura se empleaba -y aún se sigue empleando- para complementar nuestra propia y limitada memoria. Pero a veces el emisor también quería proteger sus ideas de la curiosidad de los demás, y surgía la necesidad de asegurar que el mensaje sólo iba a poder ser interpretado por ciertas personas. Había nacido la criptografía. Es cierto que en muchas ocasiones podía ser suficiente con que el mensaje estuviera escrito para que resultara indescifrable, ya que la mayoría de la gente era sencillamente analfabeta. Pero si el texto era lo suficientemente valioso, siempre se podía contratar a alguien que dominara la lengua en la que estaba escrito para que nos revelara su contenido, así que había que emplear métodos más sofisticados. El hecho que gran parte de actividades humanas sea cada vez mayor el uso de técnicas criptográficas tiene como propósito prevenir algunas faltas de seguridad en un sistema informatizado. La seguridad en general debe de ser considerada como un aspecto de gran importancia en cualquier corporación que trabaje con sistemas computarizados.  ESPARTA Y LA DIFUSION Una de las primeras técnicas criptográficas de las que se tiene noticia era la empleada por Esparta en el Siglo V antes de nuestra era. Para establecer comunicaciones militares, se empleaba un papiro alargado en forma de cinta y un bastón llamado "escitalo". El papiro se enrollaba en el bastón y se escribía el texto a lo largo de éste último, de forma transversal al papiro. Para poder leer el mensaje, el destinatario necesitaba un bastón con el mismo diámetro. Si se desea cifrar un mensaje empleando este método, y no se dispone de un bastón ni de una cinta de papiro, será suficiente con escribir el texto por columnas de tamaño fijo y luego leerlo por filas. A modo de ejemplo, el mensaje "LOS ESPARTANOS SON LOS MAS GUAPOS DEL PELOPONESO". Si se supone que el diámetro del bastón permite escribir seis signos en cada vuelta, se emplearán columnas de seis letras: Resultando: "LPO APLPOASLSO OSR O SPN TSSG EEEAO UDLSSNNMAEOO" Este criptosistema responde a un esquema de transposición, ya que lo único que se hace es cambiar de sitio los símbolos del mensaje original, por lo que si se calcula las frecuencias relativas de aparición de cada símbolo, serán iguales en el texto claro y en el criptograma. Si se tiene un texto cifrado cualquiera, y se conocen las frecuencias relativas de aparición de cada letra en el idioma del mensaje, bastará con comparar dichas frecuencias con las del criptograma para saber si ha sido codificado mediante transposiciones. ¿Se puede criptoanalizar este método?. Obviamente, se puede decodificar el mensaje en columnas de diferentes longitudes hasta dar con el mensaje original, pero habría que leer todos los posibles resultados para saber cuál es el bueno. El interés será automatizar este proceso, y para ello se puede recurrir a la redundancia. En este caso, no sirven las probabilidades de aparición de cada símbolo, puesto que, como ya se ha dicho, son las mismas en el mensaje original y en el mensaje cifrado. Sin embargo, a poco que se observe, las frecuencias relativas de las parejas y tríos de letras en el mensaje original y el criptograma sí que son diferentes, así que se explotará esa posibilidad. La idea es muy simple, en el mensaje cifrado de arriba hay combinaciones de letras que no son en absoluto frecuentes (o no permitidas) en castellano, como por ejemplo "TSS", "EEE" o "SR". Si se precalculan en una tabla las frecuencias de aparición de parejas y tríos de letras en castellano, se tendrá una distribución de probabilidad a la que deberá ajustarse el texto que dio lugar al mensaje cifrado. Esto permitirá "puntuar" cada posible texto claro en función de que su distribución se ajuste mejor o peor a la distribución estándar de pares y tríos. En el ejemplo de arriba, el mensaje tiene 48 caracteres, por lo que las columnas pueden ser de 2,3,4,6,8,12,16 o 24 caracteres de altura. Columnas de altura 2: Los símbolos de 24 en 24: "L PTOS SAGP..." No es necesario seguir, ya que por ejemplo hay una 'L' sola, que no tiene sentido en castellano.Se podrían terminar todas las posibilidades y la respuesta más verosímil es la que corresponde a columnas de altura 6. En general, en casi todas las demás posibles soluciones aparecerán combinaciones de letras muy poco probables o ilegales en castellano, por lo que el nivel de confianza es mucho menor. Un programa que realice estos cálculos y que presente las posibles soluciones ordenadas de mayor a menor verosimilitud, devolverá la solución correcta siempre en las primeras posiciones. Casi 2500 años después, Claude Shannon definió el concepto de difusión como el proceso que "dispersa la redundancia del texto plano repartiéndola a lo largo del texto cifrado". La transposición es el mecanismo más simple para llevar a cabo una difusión sobre el texto en claro. De hecho, al cambiar de sitio las cosas, pero sin alterar su valor, estamos esparciendo a lo largo del criptograma los patrones redundantes del texto original. ROMA Y LA CONFUSION Varios siglos después que la ciudad de Esparta, Cayo Julio César (100-44 ane) desarrolló su propio mecanismo de codificación de mensajes, un método que ha conservado el nombre de su creador hasta nuestros días. Este algoritmo consistía en la sustitución de cada letra por la que aparece tres posiciones a su derecha en el alfabeto, así la A se convierte en D, la B en E y así sucesivamente. Claude Shannon acuñó también un término que tiene mucho que ver con los mecanismos involucrados en este algoritmo: la confusión, que es el proceso que "oculta la relación entre el texto claro y el texto cifrado". Y como de nuevo cabría esperar, el método más simple para aplicar confusión es, precisamente, la sustitución. Para percatarse de esto basta con pensar en una sustitución global, que a cada posible mensaje le haga corresponder un criptograma diferente, mediante una simple tabla de traducción. Como es de esperar, semejante tabla sería inconcebiblemente grande, ya que tendría que tener una entrada para cada posible mensaje susceptible de ser codificado, pero proporcionaría un nivel de seguridad total, ya que no queda ningún tipo de relación entre cada mensaje y su criptograma correspondiente al margen de la gigantesca tabla. ALGORITMOS MODERNOS En la actualidad, los conceptos de confusión y difusión son la base de la inmensa mayoría de los algoritmos de cifrado simétrico que se conocen. Y es que esencialmente, un algoritmo de cifrado de este tipo es una sucesión más o menos compleja de sustituciones y transposiciones. UN POCO DE PRACTICA Se propone un reto para pasar rato entretenido. No se indica el método de codificación, así que se deberá adivinar, aunque una pista es que hay confusión y difusión. Se han cambiado los espacios por guiones y el mensaje está en varias líneas. El criptograma en cuestión es: UJQFWWPF-P-EDEKG-QGG-CNFETGQG-F-N- NFGQWGTPOGGFNDC-UPCGNVRUNGQW- R-QPPCTTV--UUXGC-V--CGCNC-EGTDGQJGF-FCSSCTQCP-CPQ FISGONES ¿Podría realmente un único avance científico hacer que todas las comunicaciones seguras dentro del planeta quedaran virtualmente expuestas? La respuesta es, curiosamente, afirmativa, y se debe a la propia naturaleza de los algoritmos criptográficos involucrados en el tema. 3.- Criptografía Simétrica  La criptografía simétrica se refiere al conjunto de métodos que permiten tener comunicación segura entre las partes siempre y cuando anteriormente se hayan intercambiado la clave correspondiente que llamaremos clave simétrica. La simetría se refiere a que las partes tienen la misma llave tanto para cifrar como para descifrar. La criptografía simétrica se refiere al conjunto de métodos que permiten tener comunicación segura entre las partes siempre y cuando anteriormente se hayan intercambiado la clave correspondiente que llamaremos clave simétrica. La simetría se refiere a que las partes tienen la misma llave tanto para cifrar como para descifrar. Este tipo de criptografía se conoce también como criptografía de clave privada o criptografía de llave privada.
Este tipo de criptografía se conoce también como criptografía de clave privada o criptografía de llave privada.
Existe una clasificación de este tipo de criptografía en tres familias, la criptografía simétrica de bloques (block cipher), la criptografía simétrica de lluvia (stream cipher) y la criptografia simétrica de resumen (hash functions). Aunque con ligeras modificaciones un sistema de criptografía simétrica de bloques puede modificarse para convertirse en alguna de las otras dos formas, sin embargo es importante verlas por separado dado que se usan en diferentes aplicaciones. La criptografía simétrica ha sido la más usada en toda la historia, ésta ha podido ser implementada en diferente dispositivos, manuales, mecánicos, eléctricos, hasta los algoritmos actuales que son programables en cualquier ordenador. La idea general es aplicar diferentes funciones al mensaje que se quiere cifrar de tal modo que solo conociendo una clave pueda aplicarse de forma inversa para poder así descifrar. Aunque no existe un tipo de diseño estándar, quizá el más popular es el de Fiestel, que consiste esencialmente en aplicar un número finito de interacciones de cierta forma, que finalmente da como resultado el mensaje cifrado. Este es el caso del sistema criptográfico simétrico más conocido, DES. DES Es un sistema criptográfico, que toma como entrada un bloque de 64 bits del mensaje y este se somete a 16 interacciones, una clave de 56 bits, en la práctica el bloque de la clave tiene 64 bits, ya que a cada conjunto de 7 bits se le agrega un bit que puede ser usado como de paridad. Dependiendo de la naturaleza de la aplicación DES tiene cuatro modos de operación para poder implementarse: ECB (Electronic Codebook Mode) para mensajes cortos, de menos de 64 bits, CBC (Cipher Block Chaining Mode) para mensajes largos, CFB (Cipher Block Feedback) para cifrar bit por bit ó byte por byte y el OFB (Output Feedback Mode) el mismo uso pero evitando propagación de error. En la actualidad no se ha podido romper el sistema DES desde la perspectiva de poder deducir la clave simétrica a partir de la información interceptada, sin embargo con un método a fuerza bruta, es decir probando alrededor de 256 posibles claves, se pudo romper DES en Enero de 1999. Lo anterior quiere decir que, es posible obtener la clave del sistema DES en un tiempo relativamente corto, por lo que lo hace inseguro para propósitos de alta seguridad. La opción que se ha tomado para poder suplantar a DES ha sido usar lo que se conoce como cifrado múltiple, es decir aplicar varias veces el mismo algoritmo para fortalecer la longitud de la clave, esto ha tomado la forma de un nuevo sistema de cifrado que se conoce actualmente como triple-DES o TDES. TDES El funcionamiento de TDES consiste en aplicar tres veces DES de la siguiente manera: la primera vez se usa una clave K1(azul) junto con el bloque B0, de forma ordinaria E (de encripción), obteniendo el bloque B1. La segunda ves se toma a B1 con la clave K2 (roja), diferente a K1 de forma inversa, llamada D (de descencripción) y la tercera vez a B2 con una clave K3 (verde) diferente a K1 y K2, de forma ordinaria E (de encripción), es decir, aplica de la interacción 1 a la 16 a B0 con la clave K1, después aplica de la 16 a la 1, a B1 con la clave K2, finalmente aplica una vez más de la 1 a la 16 a B2 usando la clave K3, obteniendo finalmente a B3. En cada una de estas tres veces aplica el modo de operación más adecuado. El proceso del cifrado con TDES se puede apreciar en las siguientes figuras: 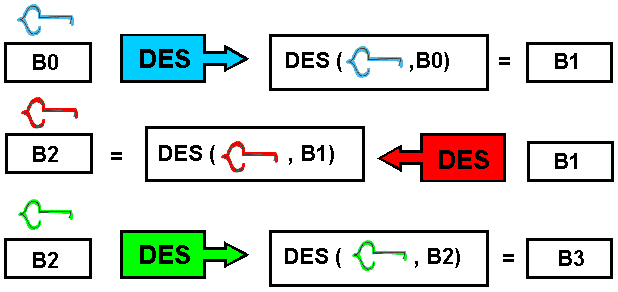 Este sistema TDES usa entonces una clave de 168 bits, aunque se ha podido mostrar que los ataques actualmente pueden romper a TDES con una complejidad de 2112, es decir efectuar al menos 2112 operaciones para obtener la clave a fuerza bruta, además de la memoria requerida. Se optó por TDES ya que es muy fácil Interoperar con DES y proporciona seguridad a mediano plazo. En los últimos 20 años se han diseñado una gran cantidad de sistemas criptográficos simétricos, entre algunos de ellos están: RC-5, IDEA, FEAL, LOKI'91, DESX, Blowfish, CAST, GOST, etcétera. Sin embargo no han tenido el alcance de DES, a pesar de que algunos de ellos tienen mejores propiedades. Podemos afirmar que el estado actual de la criptografía simétrica es la búsqueda de un nuevo sistema que pueda reemplazar a DES en la mayor parte de aplicaciones. Es así como se ha optado por convocar a un concurso de sistemas criptográficos simétricos y que se decida cual será el nuevo estándar al menos para los próximos 20 años. AES El NIST (National Institute of Standards Technology) convocó a un concurso para poder tener un sistema simétrico que sea seguro y pueda usarse al menos en los próximos 20 años como estándar. En la mitad del año de 1998 se aceptaron 15 candidatos, estos se han sometido a pruebas públicas y por parte del NIST. Posteriormente se llegó a cinco finalistas: MARS, RC6, Rijndael, Serpent y Twofish. Las principales características que se pidió a AES es que al menos sea tan seguro y rápido como TDES, es decir, que al menos evite los ataques conocidos. Además de que pueda ser implementado en una gran parte de aplicaciones. AES puede ser usado tanto como cifrador de bloques (block cipher), como cifrador de lluvia (stream cipher), como función resumen (hash function), y como generador de números pseudoaleatorios. El elegido en noviembre de 2000 por AES fue el propuesto por Rijndael. Los cifradores de flujo o "stream ciphers", son usados donde se cuente con un ancho de banda restringido (el número de bits que se transmiten a la vez), además de que se requiere independencia en los bloques transmitidos, entonces la mejor opción es cifrar bit por bit o byte por byte, este tipo de cifradores tiene la característica además de ser muy rápido. Los algoritmos más conocidos de este tipo están RC-4, SEAL y WAKE. Entre los ataques más potentes a la criptografía simétrica están el criptoanálisis diferencial y lineal, sin embargo no han podido ser muy eficientes en la práctica por lo tanto, por el momento después de que un sistema criptografíco es publicado y se muestra inmune a estos dos tipos de ataques (y algunos otros más) la mayor preocupación es la longitud de las claves. 4.- Funciones Hash Una herramienta fundamental en la cripotografía, son las funciones hash, son usadas principalmente para resolver el problema de la integridad de los mensajes, así como la autenticidad de mensajes y de su origen. Una función hash es también ampliamente usada para la firma digital, ya que los documentos a firmar son en general demasiado grandes, la función hash les asocia una cadena de longitud 160 bits que los hace más manejables para el propósito de firma digital. De forma gráfica la función hash efectúa lo siguiente: un mensaje de longitud arbitraria lo transforma de forma "única" a un mensaje de longitud constante. 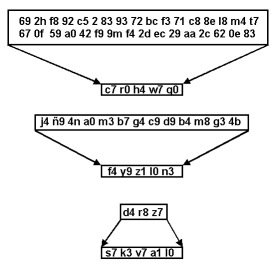 ¿Cómo hace esto? La idea general es la siguiente: La función hash toma como entrada una cadena de longitud arbitraria, digamos 5259 bits, luego divide éste mensaje en pedazos iguales, digamos de 160 bits, como en este caso y en general el mensaje original no será un múltiplo de 160, entonces para completar un número entero de pedazos de 160 bits al último se le agrega un relleno, digamos de puros ceros. En nuestro caso en 5259 caben 32 pedazos de 160 bits y sobran 139, entonces se agregarán 21 ceros más. El mensaje toma la forma X = X1, X2, X3,…,Xt donde cada Xi tiene igual longitud (160 bits por ejemplo). Posteriormente se asocia un valor constante a un vector inicial IV y H0=IV Ahora se obtiene H1 que es el resultado de combinar H0 con X1 usando una función de compresión f H1 = f(H0,X1) Posteriormente se obtiene H2, combinando H1 y X2 con f H2 = f(H1,X2) Se hace lo mismo para obtener H3 H3 = f(H2,X3) Hasta llegar a Ht Ht = f(Ht-1, Xt) Entonces el valor hash será h(M) = Ht De alguna forma lo que se hace es tomar el mensaje partirlo en pedazos de longitud constante y combinar de alguna forma pedazo por pedazo hasta obtener un mensaje único de longitud fija como muestra la figura siguiente:  Los MDC sirven para resolver el problema de la integridad de la información, al mensaje se le aplica un MDC (una función hash) y se manda junto con el propio mensaje, al recibirlo el receptor aplica la función hash al mensaje y comprueba que sea igual al hash que se envió antes. Es decir, se aplica un hash al mensaje M y se envía con el mensaje (M, h(M)), cuando se recibe se le aplica una vez más el hash (ya que M es público) obteniendo h'(M), si h(M)=h'(M), entonces se acepta que el mensaje sea transmitido sin alteración.  De forma simple se muestra en la siguiente figura el funcionamiento de un MAC. 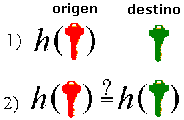
Consideremos un esquema de firma digital con apéndice, entonces la firma se aplica a h(x), en este caso h debe ser un MDC con resistencia a una 2° preimagen, ya que de lo contrario un atacante C que conozca la firma sobre h(x), puede encontrar otro mensaje x' tal que h(x) = h(x') y reclamar que la firma es del documento x'. Si el atacante C puede hacer que el usuario firme un mensaje, entonces el atacante puede encontrar una colisión (x, x') (en lugar de lo más difícil que es encontrar una segunda preimagen de x) y hacer firmar al usuario a x diciendo que firmo x'. En este caso es necesaria la propiedad de resistencia a colisión. Por último si (e,n) es la clave pública RSA de A, C puede elegir aleatoriamente un y y calcular z = ye mod n, y reclamar que y es la firma de z, si C puede encontrar una preimagen x tal que z = h(x), donde x es importante para A. Esto es evitable si h es resistente a preimagen. Las funciones hash más conocidas son las siguientes: las que se crean a partir de un block cipher como DES, MD5 ], SHA-1 y RIPEMD 160. Actualmente se ha podido encontrar debilidades en las funciones hash que tienen como salida una cadena de 128 bits, por lo que se ha recomendado usar salidas de 160 bits. Así mismo se han encontrado ataques a MD5 y SHA-0 (antecesora de SHA-1), esto ha dado lugar que se dirija la atención sobre la función has RIPEMD-160. El ataque más conocido (a fuerza bruta) a una función hash es conocido como "birthday attack" y se basa en la siguiente paradoja, si hay 23 personas en un local existe una probabilidad de al menos 1/2, de que existan dos personas con el mismo cumpleaños. Aunque parezca muy difícil esa posibilidad se puede mostrar que en general al recorre la raíz cuadrada del número de un conjunto de datos, se tiene la probabilidad de al menos ½ de encontrar dos iguales. Al aplicar esto a una función hash, es necesario recorrer entonces la raíz cuadrada de 2160 mensajes para poder encontrar dos con el mismo hash, o sea encontrar una colisión. Por lo tanto una función hash son salida 2160 tiene una complejidad de 280, y una función de 128 bits de salida tiene una complejidad de 264, por lo que es recomendable usar actualmente salida de 160 bits (48 dígitos). La criptografía simétrica, es claramente insuficiente para llevar a cabo comunicaciones seguras a través de canales inseguros -léase internet-, debido a que los dos interlocutores necesitan compartir una clave secreta -llamada "clave de sesión"-. Dicha clave debe ser transmitida en algún momento desde un extremo a otro del canal de comunicación de forma segura, ya que de ella depende la protección de toda la información que se transmita a lo largo de esa sesión en particular.Se necesita, pues, un canal seguro para poder crear otro canal seguro. Es la pescadilla que se muerde la cola. La criptografía asimétrica ofrece una salida al problema, proporcionando ese canal seguro de comunicación que va a permitir a los participantes intercambiar las claves de sesión. Y ésa no es la única ventaja, ya que los algoritmos asimétricos ofrecen mecanismos fiables para que ambos interlocutores se puedan identificar frente al otro de manera segura. La razón por la que no se emplean algoritmos asimétricos todo el tiempo es porque, entre otras ventajas, los criptosistemas simétricos resultan mucho más eficaces y rápidos. 5.- Criptografía Asimétrica La criptografía asimétrica, es por definición, aquella que utiliza dos claves diferentes para cada usuario, una para cifrar que se le llama clave pública y otra para descifrar que es la clave privada. El nacimiento de la criptografía asimétrica se dio al estar buscando un modo más práctico de intercambiar las llaves simétricas. Diffie y Hellman, proponen una forma para hacer esto, sin embargo no fue hasta que el popular método de Rivest Shamir y Adleman RSA publicado en 1978, cuando toma forma la criptografía asimétrica, su funcionamiento esta basado en la imposibilidad computacional de factorizar números enteros grandes. Actualmente la criptografía asimétrica es muy usada, sus dos principales aplicaciones son el intercambio de claves privadas y la firma digital, una firma digital se puede definir como una cadena de caracteres que se agrega a un archivo digital que hace el mismo papel que la firma convencional que se escribe en un documento de papel ordinario. Los fundamentos de la criptografía asimétrica pertenecen a la teoría de números. En la actualidad la criptografía asimétrica o de clave pública se divide en tres familias según el problema matemático del cual basan su seguridad. La primera familia es la que basa su seguridad en el Problema de Factorización Entera PFE , los sistemas que pertenecen a esta familia son, el sistema RSA, y el de Rabin Williams RW . La segunda familia es la que basa su seguridad en el Problema del Logaritmo Discreto PLD, a esta familia pertenece el sistema de Diffie Hellman DH de intercambio de claves y el sistema DSA de firma digital. La tercera familia es la que basa su seguridad en el Problema del Logaritmo Discreto Elíptico PLDE, en este caso hay varios esquemas tanto de intercambio de claves como de firma digital que existen como el DHE (Diffie Hellman Elíptico), DSAE, (Nyberg-Rueppel) NRE, (Menezes, Qu, Vanstone) MQV , etc. Aunque los sistemas asimétricos más conocidos pertenecen a las familias anteriores, existen otro tipo de sistemas que basan su seguridad en problemas diferentes como por ejemplo, en el Problema del Logaritmo Discreto Hiperelíptico, sobre problemas de retículas y sobre subconjuntos de clases de campos numéricos reales y complejos. RSA En el caso de RSA el problema matemático es el de la factorización de un número entero n grande (1024 bits), este número entero se sabe es producto de dos números primos p,q de la misma longitud, entonces la clave pública es el número n y la privada es p,q. El razonamiento del funcionamiento de RSA es el siguiente:
   Esquema de cifrado RSA Uso: este esquema se usa principalmente en cifrar claves de sistemas simétricos (claves de 128 bits aprox.)
Generación de parámetros
Proceso de cifrado Proceso de descifrado FACTORIZACIÓN Y LOGARITMOS DISCRETOS Curiosamente, la inmensa mayoría de los algoritmos asimétricos que se usan en la actualidad -por no decir todos- se apoyan en problemas como el de la factorización o el de los logaritmos discretos. En realidad existen otros algoritmos que se basan en teorías diferentes, pero hoy por hoy no están suficientemente estudiados como para ser considerados seguros de forma general, por lo que no se suelen emplear en la práctica. Sistemas como RSA, Diffie-Hellman, e incluso la criptografía de curva elíptica depositan su seguridad en estos dos problemas. Todos ellos descansan en la supuesta imposibilidad de resolverlos de forma algorítmicamente eficiente, y se dice "supuesta" porque nadie ha demostrado que no pueda existir un algoritmo capaz de hacerlo de forma satisfactoria. El problema de la factorización es justo el inverso a la multiplicación. Si para multiplicar se parte de la existencia de dos números y se trata de hallar su producto (para lo cual existen algoritmos claramente definidos), en el caso de la factorización se parte de un número y se trata de hallar sus factores primos. Por ejemplo, si se tiene el 342, se llega a que 342=2*3*3*19. Desgraciadamente (o afortunadamente, según se mire) no se conoce ningún algoritmo capaz de hacer esto de forma rápida y eficiente cuando el número a factorizar es muy grande. El problema del logaritmo discreto es algo más complejo. Se define sobre aritmética modular y consiste en averiguar cuántas veces que hay que multiplicar un número consigo mismo para que nos dé otro concreto. Por ejemplo, el logaritmo base 4 de 12 módulo 13 es el número de veces que hay que multiplicar el 4 por sí mismo para que nos dé 12 módulo 13. El resultado es 3, ya que 4*4*4=64 =12 mod 13. (lo de "módulo 13" significa tomar el resto de la división por 13). De todas formas, existe una íntima relación entre este problema y el anterior, hasta tal punto que basta con tener resuelto uno de ellos para deducir una solución al otro. Llegados a este punto parece claro cómo funcionaría la misteriosa "caja negra". Ésta analizaría el tráfico de la red, rescatando tantas claves públicas como pudiera. Esas claves serían clasificadas según el tipo de algoritmo asimétrico sobre el que estuvieran definidas (RSA, Diffie-Hellman...), para luego resolver el problema particular de factorización que plantea cada una, lo cual nos conduce a las claves privadas correspondientes. Ahora ya sólo quedaría capturar las claves de sesión e ir decodificando las comunicaciones en tiempo real. COMPLEJIDAD ALGORITMICA Pero, ¿qué es un algoritmo "eficiente"? Alguien podría decir que cuando haya ordenadores más y más rápidos, problemas que ahora son difíciles se podrán resolver, y eso es radicalmente falso. En Teoría de Algoritmos, se define el orden de complejidad de un algoritmo como una función "O(n)" de la entrada "n". Esta medida nos dice cómo crece el tiempo de computación a medida que aumenta el tamaño de la entrada. Por ejemplo, si un algoritmo fuera cuadrático, es decir, O(n^2), se tiene que el tiempo de ejecución es proporcional al cuadrado de la entrada. Eso quiere decir que si sobre la entrada dos tarda cuatro minutos, sobre la entrada 10 debe tardar cien, sobre 1000 un millón de minutos, etc. Según esto, si se desea factorizar un número, se puede tratar de dividirlo por todos los números menores que él, uno por uno. Suponiendo que la prueba de divisibilidad se ejecutara en un tiempo constante x -simplificación que en realidad no es cierta-, el algoritmo necesitaría aproximadamente n pasos para tratar de el número n. Eso quiere decir que el programa podrá factorizar sin problemas números pequeños, pero si al ejecutarlo sobre un número de 1024 bits (el módulo de una clave típica RSA), se precisan llevar a cabo una cantidad de pasos elementales enorme. Por desgracia, es imposible construir una máquina capaz de llevar a cabo semejante computación. Si por el contrario se pudiera encontrar un algoritmo capaz de resolver el problema anterior en un número de pasos proporcional, por ejemplo, al logaritmo de n, se podría factorizar un número de 1024 bits con sólo cien veces más pasos que los que necesitaríamos para hacerlo con un número de tan sólo 10 bits. No se trata, pues, de tener máquinas más rápidas -que por supuesto ayuda- sino de investigar en algoritmos con órdenes de complejidad menores, capaces de resolver los mismos problemas en menos pasos. EL ALGORITMO RSA Y LA FACTORIZACION Para finalizar, se comenta brevemente la forma concreta en la que RSA explota el problema de la factorización. Este algoritmo está definido de tal forma que tanto la codificación como la decodificación se llevan a cabo mediante una exponenciación en aritmética modular, así: C=M^e (mod n) M=C^d (mod n) siendo C el mensaje cifrado, M el mensaje original, e la clave pública (para codificar) y d la clave privada (para decodificar). Cifrar el mensaje consistirá, pues, en elevarlo a la clave pública y luego quedarse con el resto que sale al dividir por n. Para que se cumpla esta relación, debe darse la siguiente propiedad: e*d=1 (mod Ø(n)) donde Ø(n) es la llamada función Totient de Euler. Curiosamente, esta función es muy fácil de calcular si se conocen los factores de n, y muy difícil en el caso contrario. De hecho, si n=p*q, Ø(n)=(p-1)*(q-1). Puesto que la clave pública ha de estar constituida por el par (n,e) para que alguien pueda cifrar un mensaje, si fuera posible factorizar n, el algoritmo RSA estaría sencillamente perdido. UN MENSAJE TRANQUILIZADOR Afortunadamente, los matemáticos cada vez están más seguros de que los problemas en los que descansa casi toda la criptografía asimétrica conocida (y ciertamente toda la que se usa en la práctica) son computacionalmente intratables, por lo que no es posible llevarse ninguna desagradable sorpresa al respecto en los próximos años. De todas formas, hay que mantenerse en guardia y seguir investigando, porque siempre será mejor que un descubrimiento en este campo se haga en la comunidad científica y de cara al público, que en el departamento de investigación y desarrollo de una oscura agencia al servicio de algún gobierno. 6.- Otras Herramientas criptográficas En esta sección se enumeran otro tipo de herramientas o técnicas que son usadas en criptografía, cada una de ellas tiene una gran aplicación y tienen un propósito muy especifico dentro del ámbito de la criptografía, sin embargo su descripción completa no es el propósito para un lector novato así que solo se mencionarán, para un mayor estudio puede consultarse la bibliografía. Compartición de Secretos La compartición de secretos, como su nombre lo dice es una técnica criptográfica que se dedica a partir un secreto, que puede ser una clave secreta, en la responsabilidad de varias personas y que solo con el número mínimo de personas se podrá reconstruir el secreto compartido. Por ejemplo si el secreto es el número 100 y este debe ser compartido por tres personas A1, A2 y A3 una forma de poder hacerlo es generar un número aleatorio menor a 100, digamos el 33 posteriormente se genera otro número aleatorio menor a 100-33, digamos el 27, y finalmente la tercera parte será 100-(27+33)=46. Así el secreto 100 esta compartido por A1(33), A2(27) y A3(46), cada quién con su parte correspondiente. Como ninguno de ellos sabe las otras partes, solo los tres juntos podrán reconstruir el mensaje sumando sus partes. Claro está es solo un ejemplo para explicar el concepto. La comparición de secretos puede ser usada para compartir digamos la combinación de una caja fuerte, la clave de lanzamiento de algún proyectil, la clave secreta de una autoridad certificadora, la clave de activación de algún dispositivo de alto riesgo, etc.,  Uno de los mejores métodos de compartición de secretos y más conocido es el esquema (n,k) límite de Shamir. Consiste en partir una clave K en n partes, y se tiene como mínimo (límite) el número k de partes para reconstruir la clave, es decir cualquiera k de los n custodios pueden reconstruir la clave K, pero ningún subgrupo de k-1 custodios podrá hacerlo. Un ejemplo simple de esquema de Shamir se basa en lo siguiente:
donde el coeficiente es aleatorio y 2 el secreto a compartir En nuestro caso el secreto se puede reconstruir de la siguiente formula: s = c1 y1 + c2 y2 donde y1 ,y2 son las partes (5 y el 8) y c1=2, c2= -1. El secreto es entonces 2(5)-(8)=2. Criptografía Visual Una idea ingeniosa de usar un método de comparición de secretos con un esquemas límite (n,k) es la criptografía visual, esto consiste en lo siguiente: una imagen se divide en n partes, y si se sobreponen al menos k de estas partes se puede reconstruir la imagen. Veamos en ejemplo de un esquema (2,2), esto trabaja considerando que si la imagen es de blanco y negro, entonces la imagen podrá ser un conjunto de cuadros completamente blancos y completamente negros, por ejemplo la siguiente imagen  Ahora cada cuadro de la imagen podrá ser considerado como blanco o negro, equivalentemente con valores 0 y 1. Para partir esta imagen en dos partes n=2 y considerando el límite con k=2, se procede como sigue: Cada cuadro que es completamente negro podrá ser partido en dos partes de la siguiente forma: 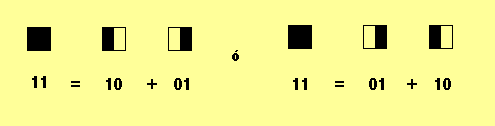 Y un cuadro completamente blando podrá ser partido en dos de la forma siguiente: 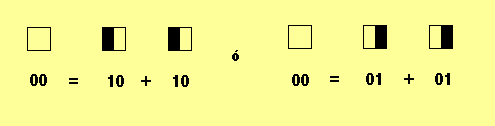 Que significa suma módulo 2, es decir 1+0=1, 0+1=1, 0+0=0 pero también 1+1=0, de este modo se pueden tomar cualquiera de las dos particiones de los cuadros de color blanco. Para formar las dos partes de la figura en un acetato se elige aleatoriamente una de las combinaciones anteriores según se parta un cuadro blanco o uno negro En el caso de nuestra figura una ves elegidas las partes, la figura partida en un esquema limite (2,2) queda así:   Parte 2 De esta forma se tiene partida la figura en dos partes y se recuperara solo sobreponiendo una sobre la otra. Al sobreponer las dos partes se recupera la figura, de la siguiente forma:  En el caso general se parte los cuadros blancos y negros en n pedazos y hasta no tener k pedazos negros el cuadro reconstruido será siendo blanco, a partir de k pedazos negros hasta n el cuadro reconstruido será negro. En nuestro caso, un cuadro con solo la mitad negra será considerado blanco, es necesario que tenga dos mitades negras para que el cuadro reconstruido se considere negro, que es el caso del esquema (2,2). Dinero Electrónico Una aplicación más, que puede ser realidad gracias a la criptografía de clave pública es conocida como dinero electrónico, en términos sencillos el dinero electrónico es otra representación de lo que conocemos como dinero o valor, por ejemplo tenemos dinero en billetes emitidos por algún país, podemos tener cheques pagaderos en un banco, bonos, pagarés pagaderos en algún plazo, en fin. El dinero electrónico es físicamente un número que se genera aleatoriamente, se le asigna un valor, se cifra y firma y se envía al banco, ahí el banco valida el número y certifica el valor, y lo retorna al usuario firmado por el banco, entonces el usuario puede efectuar alguna transacción con ese billete electrónico.  Las principales propiedades del dinero electrónico son las siguientes:
Supóngase que el usuario A quiere mandar un cheque a B, usando ahora dinero electrónico.
En el mundo comercial existen varias empresas privadas que proveen el servicio de dinero electrónico en diferentes modalidades entre ellas están: CheckFree, CyberCash, DigiCash, First Virtual, Open Market, NetBill y Netscape. En http://www.ecashtechnologies.com/ pueden encontrarse algunos ejemplos interactivos de cómo trabaja el dinero electrónico en la práctica 7.- Certificados digitales Los certificados digitales, tienen una similitud con las licencias de conducir, las primeras permiten viajar por las carreteras, los certificados digitales permiten navegar por internet, la principal característica es que da identidad al usuario y puede navegar con seguridad. De igual forma que la licencia de conducir o un pasaporte sirve para dar identidad a quien la porta en ciertos casos, el certificado digital da identidad a una clave pública y se comporta como una persona en el espacio cibernético. El nacimiento del certificado digital fue a raíz de resolver el problema de administrar las claves públicas y que la identidad del dueño no pueda ser falsificada. La idea es que una tercera entidad intervenga en la administración de las claves públicas y asegure que las claves públicas tengan asociado un usuario claramente identificado. Esto fue inicialmente planteado por Kohnfelder del MIT en su tesis de licenciatura. Las tres partes más importantes de un certificado digital son: En la actualidad casi todas las aplicaciones de comercio electrónico y transacciones seguras requieren un certificado digital, se ha propagado tanto su uso que se tiene ya un formato estándar de certificado digital, este es conocido como X509 v. 3 Algunos de los datos más importantes de este formato son los siguientes:
Un certificado digital entonces se reduce a un archivo de uno o dos koctetos de tamaño, que autentica a un usuario de la red. En una aplicación un certificado digital se puede ver como la siguiente pantalla:  8.- Infraestructura de claves públicas Teniendo ya un certificado digital que es generado con la ayuda de un algoritmo de clave pública ahora el problema es como administración todos estos, la estructura más básica es la siguiente: 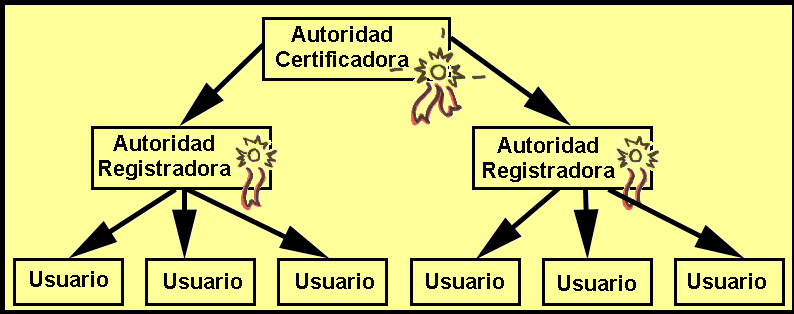 El papel de la Autoridad certificadora (AC) es de firmar los certificados digitales de los usuarios, generar los certificados, mantener el status correcto de los certificados, esto cumple el siguiente ciclo:
Generar certificadosEntre las que pudiera realizar una AR están: Recibir las solicitudes de certificaciónY las actividades de los usuarios: Solicitar el certificadoUna ves que algún usuario tiene un certificado digital este puede usarlo para poder navegar por la red con nombre y apellido en forma de bits, esto permite entrar al mundo del comercio electrónico, al mundo de las finanzas electrónicas y en general a la vida cibernética con personalidad certificada. El usuario dueño de un certificado digital tiene la potencialidad de poder autentificarse con cualquier otra entidad usuaria, también puede intercambiar información de forma confidencial y estar seguro de que esta es íntegra, así estar seguro que contactos vía el certificado digital no serán rechazados. Los primeros usuarios de certificados digitales fueron los servidores, actualmente son quienes más los usan, sin embargo también se ha incrementado el número de personas que los usan. Si suponemos que algún tipo de aplicación funciona ya con certificados digitales, esta tendrá una AC y las correspondientes AR, sin embargo es común que haya mas autoridades certificadoras y que sus usuarios puedan interoperar con sus respectivos certificados, a esto se le conoce como certificación cruzada y opera de la siguiente forma: 1) Las diferentes AC pueden estar certificadas enviándose una a otra sus respectivos certificados que ellas mismas generan 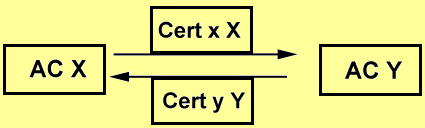
 Las operaciones de la administración de los certificados digitales puede cambiar de acuerdo a las leyes particulares de cada país o entidad. 9.- Comercio electrónico Hoy en día, gran parte de la actividad comercial ha podido transformarse gracias a redes de conexión por ordenadores como Internet, esta transformación facilita hacer transacciones en cualquier momento, de cualquier lugar del mundo. Todo lo que esta alrededor de esta nueva forma de hacer negocios es lo que se ha llamado comercio electrónico, sin duda la gran variedad de actividades que giraban alrededor del quehacer comercial se ha tenido que juntar con las nuevas técnicas cibernéticas. Así hoy tanto un comerciante, un banquero, un abogado o una matemático puede hablar de comercio electrónico enfocándose a la parte que le corresponde.  Existen diferentes niveles de hacer comercio electrónico, y su clasificación aún esta por formarse, sin embargo, la parte más visible es la que cualquier usuario en una computadora personal puede ver, esto es hacer comercio electrónico se convierte a comprar o vender usando una conexión por Internet en lugar de ir a la tienda. La forma de hacer esto es muy similar a lo que tradicionalmente se hace, por ejemplo: en la tienda uno entra al establecimiento, de forma electrónica se prende el ordenador y una ves conectado a Internet entra a la página del negocio, enseguida un comprador revisa los productos que posiblemente compre y los coloca en una carrito, de la misma forma en la computadora se navega por la página del negocio y con el browser se revisa los productos que éste vende, al escoger éstos se colocan en un carrito virtual, que no es nada mas que un archivo del usuario. Una vez elegido bien los productos de compra se pasa a la caja, donde se elige un sistema de pago y se facturan los productos al comprador. De forma similar en la computadora se pueden borrar productos que no se quieren comprar o añadir nuevos, una ves elegidos éstos se procede a una parte de la pagina que toma los datos y solicita el método de pago, generalmente se lleva a cabo con tarjeta de crédito. En la parte tradicional de comprar al pagar en la caja termina el proceso, en la parte por ordenador aún tiene que esperarse que sean enviados los productos. A pesar de esto las ventajas que ofrece el comercio electrónico son magníficas, ya que es posible comprar en un relativo corto tiempo una gran cantidad de productos sin necesidad de moverse de lugar, es decir al mismo tiempo se puede comprar una computadora, un libro, un regalo, una pizza, hacer una transacción bancaria etc., de la forma tradicional se llevaría al menos un día completo y eso si los negocios esta en la misma ciudad, si no, el ahorro de tiempo que representa comprar por Internet es incalculable.  Al efectuar una operación comercial por Internet se presentan nuevos problemas, por ejemplo cómo saber que la tienda virtual existe verdaderamente, una vez hecho el pedido cómo saber que no se cambia la información, cuando se envía el número de tarjeta de crédito cómo saber si este permanecerá privado, en fin, para el comerciante también se presentan problemas similares, cómo saber que el cliente es honesto y no envía información falsa, etc. Todos estos problemas pueden ser resueltos de manera satisfactoria si se implementan protocolos de comunicación segura usando criptografía. En la siguiente sección nos dedicamos a describir como es que estos protocolos resuelven los problemas planteados. Protocolos de seguridad Un protocolo de seguridad es la parte visible de una aplicación, es el conjunto de programas y actividades programadas que cumplen con un objetivo especifico y que usan esquemas de seguridad criptográfica. El ejemplo más común es SSL (Secure Sockets Layer) (que vemos integrado en el navegador de Netscape y hace su aparición cuando el candado de la barra de herramientas se cierra y también sí la dirección de Internet cambia de http a https, otro ejemplo es PGP que es un protocolo libre ampliamente usado de intercambio de correo electrónico seguro, uno más es el conocido y muy publicitado SET que es un protocolo que permite dar seguridad en las transacciones por Internet usando tarjeta de crédito, IPsec que proporciona seguridad en la conexión de Internet a un nivel más bajo. Estos y cualquier protocolo de seguridad procura resolver algunos de los problemas de la seguridad como la integridad, la confidencialidad, la autenticación y el no rechazo, mediante sus diferentes características Las características de los protocolos se derivan de las múltiples posibilidades con que se puede romper un sistema, es decir, robar información, cambiar información, leer información no autorizada, y todo lo que se considere no autorizado por los usuarios de una comunicación por red. Enseguida vemos un escenario donde puede ocurrir algo de esto: Por ejemplo sobre la seguridad por Internet se deben de considerar las siguientes tres partes: seguridad en el navegador (Netscape, Opera, ...), la seguridad en el Web server (el servidor al cual nos conectamos) y la seguridad de la conexión. Un ejemplo de protocolo es SET, objetivo efectuar transacciones seguras con tarjeta de crédito, usa certificados digitales, criptografía de clave pública y criptografía clave privada. SSL Es el protocolo de comunicación segura más conocido y usado actualmente, SSL actúa en la capa de comunicación y es como un túnel que protege a toda la información enviada y recibida. SSL es usado en gran cantidad de aplicaciones que requieren proteger la comunicación. Con SSL se pueden usar diferentes algoritmos para las diferentes aplicaciones, por ejemplo usa DES, TDES, RC2, RC4, MD5, SHA-1, DH y RSA, cuando una comunicación esta bajo SSL la información que se cifra es: El URL del documento requeridoEl procedimiento que se lleva acabo para establecer una comunicación segura con SSL es el siguiente:
SET este protocolo esta especialmente diseñado para asegurar las transacciones por Internet que se pagan con tarjeta de crédito. Esto es debido a que una gran cantidad de transacciones de compra por Internet son efectuadas con tarjeta de crédito, por otro lado SSL deja descubierto alguna información sensible cuando se usa para lo mismo. La principal característica de SET, es que cubre estos huecos en la seguridad que deja SSL. Por ejemplo con SSL solo protege el número de tarjeta cuando se envía del cliente al comerciante, sin embargo no hace nada para la validación del número de tarjeta, para chequear sí el cliente esta autorizado a usar ese número de tarjeta, para ver la autorización de la transacción del banco del comerciante etc., Además que el comerciante puede fácilmente guardar el número de tarjeta del cliente. En fin todas estas debilidades son cubiertas por SET, éste permite dar seguridad tanto al cliente, al comerciante como al banco emisor de la tarjeta y al banco del comerciante. El proceso de SET es más o menos el siguiente:
10.- Vocabulario Privacidad: se refiere a tener control en el acceso de la información y solo permitirlo a personas autorizadas Autenticidad: se refiere a estar seguros de la identidad de una entidad ya sea mensaje, persona, servidor etc. Integridad: se refiere a que la información no sea modificada No-rechazo: se refiere a no poder negar la autoría de un mensaje o de una transacción. Criptografía: es el conjunto de técnicas (entre algoritmos y métodos matemáticos) que resuelven los problemas de autenticidad, privacidad, integridad y no rechazo en la transmisión de la información. Texto original: es un documento antes de ser cifrado Cifrar: es la acción que produce un texto cifrado (Ilegible) a partir de un texto original Texto cifrado: es un documento que ha sido cifrado Descifrar: es la acción inversa de cifrar, es decir, convierte un texto cifrado a otro legible (texto original) Firma digital: es un método que usa criptografía asimétrica y permite autenticar una entidad (persona o servidor), tiene una función igual que la firma convencional. Consiste en dos procesos, uno de firma y otro de verificación de la firma. Físicamente es una cadena de caracteres que se adjunta al documento. Criptografía simétrica: es el conjunto de métodos que permite establecer comunicación cifrada, con la propiedad de que ambos lados de la comunicación tienen la misma clave, y ésta es secreta. Criptografía asimétrica: es el conjunto de métodos que permite establecer comunicación cifrada, donde una de las claves es pública y la otra clave es privada (secreta). Cada usuario tiene un par de claves una pública y otra privada. Clave privada: es la clave secreta que se usa en la criptografía asimétrica Clave pública: es la clave públicamente conocida, que se usa en la criptografía asimétrica Clave simétrica: es la clave secreta que tienen ambos lados de una comunicación en la criptografía simétrica. Par de claves: se refiere al par de claves una privada y otra pública usadas en la criptografía asimétrica. Longitud de la clave: es el número de bits (ceros y unos) que tienen las claves y es solo uno de los parámetros de los que depende la seguridad de un sistema criptográfico. Actualmente se usan 128 para las claves simétricas, 1024 para el sistema asimétrico RSA, 163 para los sistemas asimétricos que usan curvas elípticas. Firma digital con apéndice: método de firma digital que requiere al mensaje como entrada en el proceso de verificación. Firma digital con mensaje recuperable: método de firma digital que no requiere al mensaje como entrada en el proceso de verificación. El mensaje se recupera después de que se ha verificado la firma. Certificado digital: físicamente es un archivo de hasta 2K de tamaño que contiene principalmente, los datos de una entidad una persona o un servidor, la clave pública de esa entidad, y la firma de una autoridad certificadora que es reconocida con la capacidad de poder comprobar la identidad de la persona (o servidor) y válida la clave pública que es asociada a la entidad. Familia criptográfica: es el conjunto de sistemas criptográficos que basan su seguridad en el mismo problema matemático, actualmente las familias criptográficas más conocidas son las que basan su seguridad en el Problema de Factorización Entera (RSA, RW), los que la basan en el problema del logaritmo discreto (DH, DSA), y los que la basan en el problema del logaritmo discreto elíptico (DHE, DSAE, MQV) Función hash: es una función de un solo sentido, resistente a colisiones que asocia una archivo o documento de longitud arbitraria a una cadena de longitud constante (se usa actualmente 160b de salida), las funciones hash más conocidas son: MD5, SHA1, RIPMED 160. Cifrador de Bloque: es un sistema criptográfico que cifra de bloques en bloque, usualmente cada bloque es de 128 bits. Algunos sistemas conocido son, TDES, RC5, AES. Cifrador de Flujo: es un sistema criptográfico de cifra de bit en bit, los más conocidos son, RC4, SEAL, WAKE. Generador de números seudoaleatorios: es una función que tiene como entrada una cadena (conjunto de bits) llamada semilla y como salida otra cadena de bits que al aplicarle ciertas pruebas de aleatoriedad pasan con un porcentaje aceptable (alrededor de un 95%) Primitiva criptográfica: es la función más básica que compone un sistema criptográfico, existen la primitiva de cifrado, la primitiva de descifrado, la primitiva de firma, la primitiva de verificación de firma etc. Esquema criptográfico: es un conjunto de primitivas que componen una aplicación criptográfica más completa, como el esquema de firma digital (compuesta de la primitiva de firma y la de verificación), el esquema de cifrado (compuesta con la primitiva de cifrado y la de descifrado) etc. Protocolo (criptográfico): es la parte más visible de la aplicación y esta compuesto de esquemas criptográficos conjuntamente con otras operaciones que permiten proporcionar seguridad a una aplicación mas especifica, por ejemplo el protocolo SSL, SET, SMIME, IPsec etc. Autoridad certificadora: es una entidad (compañía) que es reconocida para poder certificar la asociación de una clave pública a una persona o servidor. Comercio electrónico: es todo lo relacionado con realizar comercio principalmente por Internet. Compartición de secretos: es un esquema criptográfico que tiene como entrada un secreto (por ejemplo una clave criptográfica) y como salida un numero n de partes del secreto y todas o algunas de éstas n partes sirven para reconstruir el secreto. Criptografía Visual: es un esquema de compartición de secretos donde el secreto es una imagen y las partes son también varias imágenes. La ventaja de este tipo de cripotgrafía es que no es necesaria una computadora para la reconstrucción del secreto. Dinero electrónico: es un número (de alrededor de 100 dígitos) al que se le asocia cierto valor y pude ser usado como cualquier otro tipo de dinero. Este número va acompañado de la firma del dueño o de un banco. Generador probabilístico de números primos: es un proceso que tiene como entrada un número entero y como salida un probable número primo con gran grado de aceptación. El método más aceptado para generar primos es el de Miller Rabin. Primo industrial: es un número primo generado probabilísticamente que tiene a lo más 1/(2^100) de probabilidad de error (de no ser número primo). Problema de Factorización: es el problema inverso a la multiplicación, es decir el problema de encontrar los factores conocido el producto. En criptografía los números a factorizar son los productos de dos números primos de la misma longitud, el producto tiene al menos 768 bits. Actualmente se han podido factorizar números de hasta 512 bits (155 dígitos) producto de dos primos del mismo tamaño (256 bits). Métodos de Factorización: es un método que tiene como entrada un número compuesto (no primo) y como salida uno de sus factores no triviales (diferentes a 1 y a el mismo). Actualmente el método más adecuado para factorizar números arbitrarios y que es usado para factorizar los números productos de dos primos es la criba de campos numéricos. Problema del Logatirmo Discreto: es el problema de encontrar el número de veces que hay que multiplicar un número conocido para obtener como resultado, otro también conocido, por ejemplo dado el 1024 y el 2, ¿cuántas veces hay que multiplicar el 2 para obtener 1024? La respuesta es 10 y se dice que 10 es el logaritmo de 1024 base 2. Métodos para calcular Logaritmos Discretos: hasta la fecha el método más adecuado para calcular logaritmos discretos es el método del Indice. Este método permite calcular logaritmos del mismo orden que las claves del sistema RSA, esto quiere decir que las claves de sistemas que usen logaritmos discretos deben de tener el mismo orden que las claves RSA. Problema del Logaritmo Discreto Elíptico: en este caso el problema es encontrar cuantas veces hay que sumar un punto racional para obtener otro conocido. Dado P y Q encontrar x, tal que xP=Q. Método para resolver el Problema del Lobaritmo Discreto Elíptico: actualmente el mejor algoritmo para calcular logaritmos discretos es el que se aplica a grupos en general llamado método de la raíz de Pollar. Problema del Logaritmo Discreto Hiperelíptico: es el problema de encontrar un número de veces que hay que sumar un divisor dado D para obtener otro divisor D'. Aritmética modular: son las operaciones de suma o producto que se llevan a cabo sobre los números enteros módulo algún entero n. Es decir el resultado de una suma o un producto es el residuo de la división entre n. Números "Grandes": se considera que un número es grande si tiene longitud al menos de 512 bits (155 dígitos), a causa de que los procesadores actuales manejan solo números de 32 bits, se tienen que diseñarse programas para poder efectuar las operaciones sobre este tipo de números. Teorema Chino del Residuo TCR: es un resultado que permite calcular la solución de ciertas ecuaciones modulares y es usado en el esquema de descifrado RSA que permite descifrar más rápidamente. Función exponencial modular: es la operación que se usa para cifrar u descifrar en varios sistemas cripotgráficos (RSA, RW, DH, DSA) y consiste en multiplicar modularmente muchas veces un mismo número. Números de Fermat: los números de Fermat son de la forma (2^(2^n)+1), el número 1 de Fermat es (2^(2^1)+1)=5, el número 2 de Fermat es (2^(2^2)+1)=17, el siguiente es (2^(2^3)+1)=257, y el 4 es (2^(2^4)+1)=65537. Fermat había afirmado que todos estos números eran primos aunque esto no es cierto. El número 4 de Fermat se usa como exponente público (e) en el sistema RSA, como su representación hexadecimal es 01 00 01 es óptimo para ser usado como exponente. Inverso multiplicativo modular: dado un número su inverso multiplicativo es el número que al multiplicarlo el resultado será uno (1). Por ejemplo en Z3 el inverso multiplicativo de 2 es 2 ya que 2*2 = 4 mod 3= 1. En los números enteros módulo otro número entero, no todos los números tienen inverso multiplicativo. En cripotgrafía la clave privada d (del sistema RSA) es precisamente el inverso multiplicativo de la parte de la clave pública e. O sea d = e-1 mod n. Campo primo (Zp): cuando en Zn, n es número primo n=p, entonces todos los elementos tienes inverso multiplicativo. Esto es tanto la suma como el producto cumplen las mismas propiedades que los números Racionales o los números Reales. En cripotgrafía es ampliamente usado este tipo de campos. Campo de característica 2 (F2n): este tipo de campos son conjuntos de n-adas (cunjuntos de ceros y uno de longitud n) a los que se les define operaciones de suma y multiplicación y tienen también las propiedades de lo números Racionales o Reales. Este tipo de campos son usados también en cripotgrafía principalmente porque es fácil fabricar un chip (circuito) que efectúa eficientemente las operaciones de suma y producto. Función de Euler (phi, j ): esta función tiene como entrada un número entero y da como resultado el número de primos relativos a n que son menores a n. Para el caso de RSA es usado phi(n) con n la clave pública, en este caso phi(n)=(p-1)(q-1) Función de Carmichael (lamda l ): esta función tiene como estrada un número entero y da como salida (para el caso n=pq) al mínimo común múltiplo de (p-1)(q-1). En el sistema RSA es usado para realizar el cifrado y descifrado más eficientemente, se asume esta función en el PKCS #1 v 2. Curva elíptica: una curva elíptica en el caso de la cripotgrafia se considera como una ecuación de dos variables de grado 3, es decir la máxima potencia de las variables debe ser 3. Por ejemplo y2=x3+2x+3 es una curva elíptica. Además de no contener puntos malos en criptografía llamados singulares. Punto racional: es una pareja (x,y) de elementos de un campo que satisfacen la ecuación de una curva elíptica. El conjunto de puntos racionales de la curva elíptica y2=x3+ax+b, se denota como E: y2=x3+ax+b. Número de puntos racionales: en un sistema criptográfico con curvas elípticas es muy importante el número de puntos racionales (llamado el orden de la curva) ya que este número debe contener como factor a un número primo de al menos 163 bits para considerar que la curva sea segura en criptografía. Curva supersingular: son curvas elípticas que por un lado tienen la propiedad de ser muy fácil calcular el número de puntos racionales pero por el otro existe un método llamado MOV (de Menezes, Okamoto, Vanstone) que permite calcular logaritmos discretos y así no son recomendables para su uso en criptografía. Curva no supersingular: son curvas elípticas que son inmunes (en la práctica) al MOV además de ser muchas curvas y son las más recomendables para el uso en cripotgrafía por los estándares actuales. Curva anómala: es una curva elíptica que tiene tantos puntos racionales como elementos tiene el campo finito (en uso), para este tipo de curvas existe un método que calcular logaritmos discretos, por que se recomienda evitarlas. Curva hiperelíptica: es una curva que generaliza a una curva elíptica y que también han sido propuestas para ser usadas en criptografía. Divisores: el papel de puntos racional de una curva elíptica lo toman los divisores. Retícula: es otro conjunto de elementos que han propuesto para ser usados en cripotografía de hecho ya existen sistemas comerciales que las usan. Campo numérico real: es un conjunto del tipo a+(d1/2) b, donde a,b son números reales y que tienen propiedades que permiten ser usados en criptografía. También existen sistemas comerciales que lo usan. |
|
Tema relacionado: Gestión de riesgos en ingeniería del softare Enlaces relacionados: Criptografía y seguridad en computadores Criptografía recreativa Información y telecomunicaciones Taller de criptografía |
|
Página de apuntes de la asignatura Informática Aplicada a la Gestión Pública(GAP). Universidad de Murcia Correo electrónico: barzana@um.es |
|
|
| www.google.es |